
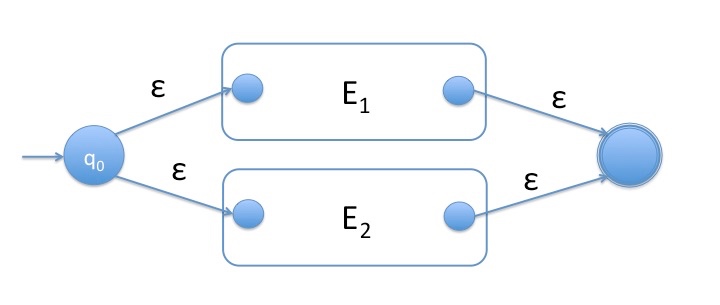
Show how to combine the automata to create a new automaton that recognizes the desired language.Build automata (dfas or nfas) for each of the languages involved.41–110.CSC 4170 Closure II Closure II: Union, Concatenation, Negation, Kleene Star, Reverse General Approach Salomaa, Chapter 2 (Springer, Heidelberg, 1997), pp. Yu, Regular languages, Handbook of Formal Languages - Vol. Nagy, Operational union-complexity, Information and Computation ( 2021) 104692. Hospodár et al., Lecture Notes in Computer Science, Vol. Nagy, Union-freeness, deterministic union-freeness and union-complexity (invited paper), DCFS 2019: Descriptional Complexity of Formal Systems, eds. Computational Intelligence and Informatics ( 2010), pp. Nagy, On union-complexity of regular languages, CINTI 2010: 11th IEEE Int. Nagy, Union-free regular languages and 1-cycle-free-path-automata, Publ. Dinnen), CDMTCS Report 252 (Auckland, 2004), pp. Nagy, A normal form for regular expressions, Supplemental Papers for DLT’04 ( 8th Int. Wendlandt, Expressive capacity of subregular expressions, RAIRO ITA: Theor.

Nagy, On union-free and deterministic union-free languages, International Federation for Information Processing - Theoretical Computer Science 2012, IFIP-TCS 2012, LNCS, Vol. Masopust, Complexity in union-free regular languages, Int. Ullman, Introduction to Automata Theory, Languages and Computation (Addison-Wesley Publishing Company, Reading MA, 1979). Kutrib, Structure and complexity of some subregular language families, The Role of Theory in Computer Science ( 2017), pp. Ésik, On equations for union-free regular languages, Inform. Descriptional Complexity of Formal Systems, DCFS 2018, eds. Davies, Most complex deterministic union-free regular languages, 20th Int.

Brzozowski, Regular expression techniques for sequential circuits, PhD Dissertation, Department of Electrical Engineering (Princeton University, Princeton, NJ, 1962).

Golomazov, Minimal union-free decompositions of regular languages, Language and Automata Theory and Applications, LNCS, Vol. This fact also allows to define n-union-complexity of regular languages. As an important result here we show that every regular language can be defined by a finite union of n-union-free languages. It is also known that the same fact does not hold for deterministic union-free languages, that is, there are regular languages that cannot be written as finite unions of d-union-free languages. It is well known that every regular expression can be written in union normal form, i.e., all regular languages can be described as finite unions of (nondeterministic) union-free languages. On the other hand, a regular expression is in union normal form if it is a finite union of union-free expressions. Some properties of the new subregular class of languages are discussed, e.g., closure properties. In case of unary alphabet the class of n-union-free languages coincides with the class of union-free languages. The defined language class is shown to be properly between the classes of (nondeterministic) union-free and d-union-free languages (in case of at least binary alphabet). In this paper λ -free nondeterministic variants of 1CFPAs are used to define n-union-free languages. The deterministic counterpart of such class of automata defines the deterministic union-free (d-union-free, for short) languages. Obviously such an automaton has exactly one accepting state. The language class is also characterised by a special class of finite automata: 1CFPAs have exactly one cycle-free accepting path from each of their states. Consequently, (nondeterministic) union-free languages are described by regular expressions using only concatenation and Kleene star. Union-free expressions are regular expressions without using the union operation.


 0 kommentar(er)
0 kommentar(er)
